数据结构 第六章 图-1
本文共 3007 字,大约阅读时间需要 10 分钟。
基本概念
图,定义为G(V, E)。集合V中的元素称作节点vertex,集合E中的元素分别对应于V中的某一对定点(u,v),表示他们之间存在某种关系,故称为边(edge)。
邻接关系:彼此之间存在关系且邻接的,顶点与顶点之间的关系。对于任何边e=(u,v),称作顶点u和v彼此邻接adjacent,互为邻居。而他们都与边e彼此关联incident。
关联关系:定点与相关的边的关系。
入度 (in-degree) :以某顶点为弧头,终止于该顶点的弧的数目称为该顶点的入度。
出度 (out-degree) :以某顶点为弧尾,起始于该顶点的弧的数目称为该顶点的出度。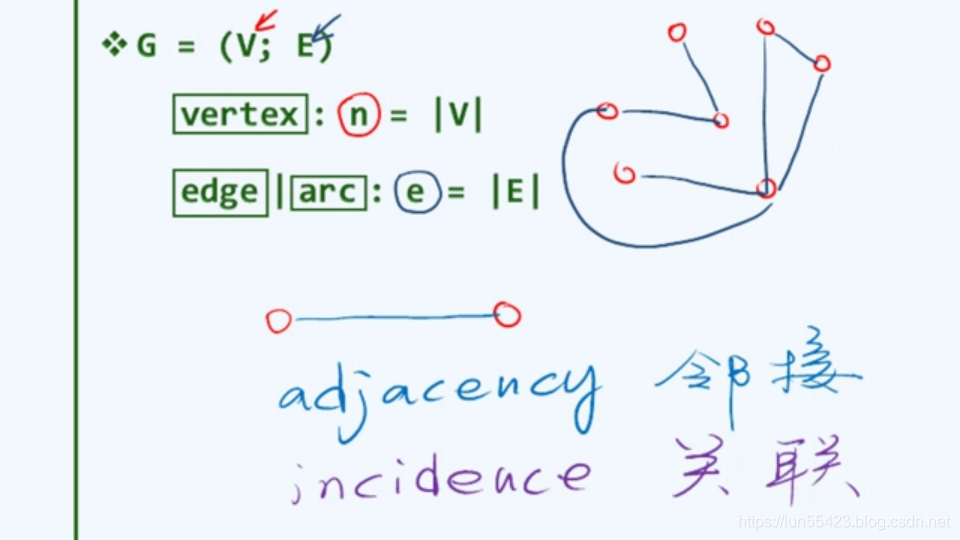
无向图,有向图及混合图
无向边:若边(u,v)所对应的定点u,v的次序无所谓,则称无向边,反之为有向边。
有向边(u,v):表示从u指向v。其中,u称作该边的起点或尾顶点,v称作该边的终点或头顶点。
无向图:所有的边都是无向边。
有向图:所有的边都是有向边。
混合图:既有有向边又有无向边。
读数(degree):在无向图中,与顶点v关联的边数,称为v的度数,记作deg(v)。
路径与通路
路径或通路(path),就是由m+1个顶点和m条边交替而成的一个序列,π={v0,e1,v1,e2....em,vm}。且对于任何0<i≤m都有ei=(Vi-1,Vi)。沿途边的总数m,称作通路的长度,记作|π|=m。
简单路径:不含重复节点的路径。simple path。
环路:对于长度m≥1,起止顶点相同的通路π,称为环路。
欧拉环路:经过图中各边一次且恰好一次的环路。
哈密顿环路:经过图中各顶点一次且恰好一次的环路。
自环:联接于同一顶点之间的边,称作自环。
带权网络:每个边都指定权重。
复杂度:通过顶点数和边的总和(n+e)来度量。
Graph模板类:
typedef enum { UNDISCOVERED, DISCOVERED, VISITED } VStatus; //顶点状态typedef enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD } EType; //边在遍历树中所属的类型template //顶点类型、边类型class Graph { //图Graph模板类private: void reset() { for ( int i = 0; i < n; i++ ) { //所有顶点的 status( i ) = UNDISCOVERED; dTime( i ) = fTime( i ) = -1; //状态,时间标签 parent( i ) = -1; priority( i ) = INT_MAX; //(在遍历树中的)父节点,优先级数 for ( int j = 0; j < n; j++ ){ //所有边的 if( exist( i, j ) ) type( i, j ) = UNDETERMINED; //类型 } } } void BFS( int, int& );//(连通域)广度优先搜索算法 void DFS( int, int& );//(连通域)深度优先搜索算法 void BCC( int, int&, Stack & );//(连通域)基于DFS的双连通分量分解算法 bool TSort( int, int&, Stack * );//(连通域)基于DFS的拓扑排序算法 template void PFS( int, PU );//(连通域)优先级搜索框架public: // 顶点 int n;//顶点总数 virtual int insert( Tv, const& ) = 0;//插入顶点,返回编号 virtual Tv remove( int ) = 0;//删除顶点及其关联边,返回该顶点信息 virtual Tv& vertex( int ) = 0;//顶点v的数据(该顶点的确存在) virtual int inDegree( int ) = 0;//顶点v的入度(该顶点的确存在) virtual int outDegree( int ) = 0;//顶点v的出度(该顶点的确存在) virtual int firstNbr( int ) = 0;//顶点v的首个邻接顶点 virtual int nextNbr ( int, int ) = 0; //顶点v的(相对于顶点j的)下一邻接顶点 virtual VStatus& status ( int ) = 0; //顶点v的状态 virtual int& dTime ( int ) = 0; //顶点v的时间标签dTime virtual int& fTime ( int ) = 0; //顶点v的时间标签fTime virtual int& parent ( int ) = 0; //顶点v在遍历树中的父亲 virtual int& priority ( int ) = 0; //顶点v在遍历树中的优先级数 // 边:这里约定,无向边均统一转化为方向互逆的一对有向边,从而将无向图视作有向图的特例 int e; //边总数 virtual bool exists ( int, int ) = 0; //边(v, u)是否存在 virtual void insert ( Te const&, int, int, int ) = 0; //在顶点v和u之间插入权重为w的边e virtual Te remove ( int, int ) = 0; //删除顶点v和u之间的边e,返回该边信息 virtual EType & type ( int, int ) = 0; //边(v, u)的类型 virtual Te& edge ( int, int ) = 0; //边(v, u)的数据(该边的确存在) virtual int& weight ( int, int ) = 0; //边(v, u)的权重 // 算法 void bfs ( int ); //广度优先搜索算法 void dfs ( int ); //深度优先搜索算法 void bcc ( int ); //基于DFS的双连通分量分解算法 Stack * tSort ( int ); //基于DFS的拓扑排序算法 void prim ( int ); //最小支撑树Prim算法 void dijkstra ( int ); //最短路径Dijkstra算法 template void pfs ( int, PU ); //优先级搜索框架};
转载地址:http://duir.baihongyu.com/
你可能感兴趣的文章
NIFI大数据进阶_内嵌ZK模式集群1_搭建过程说明---大数据之Nifi工作笔记0015
查看>>
NIFI大数据进阶_外部ZK模式集群1_实际操作搭建NIFI外部ZK模式集群---大数据之Nifi工作笔记0017
查看>>
NIFI大数据进阶_实时同步MySql的数据到Hive中去_可增量同步_实时监控MySql数据库变化_操作方法说明_01---大数据之Nifi工作笔记0033
查看>>
NIFI大数据进阶_离线同步MySql数据到HDFS_01_实际操作---大数据之Nifi工作笔记0029
查看>>
NIFI大数据进阶_离线同步MySql数据到HDFS_02_实际操作_splitjson处理器_puthdfs处理器_querydatabasetable处理器---大数据之Nifi工作笔记0030
查看>>
NIFI大数据进阶_离线同步MySql数据到HDFS_说明操作步骤---大数据之Nifi工作笔记0028
查看>>
NIFI大数据进阶_连接与关系_设置数据流负载均衡_设置背压_设置展现弯曲_介绍以及实际操作---大数据之Nifi工作笔记0027
查看>>
NIFI数据库同步_多表_特定表同时同步_实际操作_MySqlToMysql_可推广到其他数据库_Postgresql_Hbase_SqlServer等----大数据之Nifi工作笔记0053
查看>>
NIFI汉化_替换logo_二次开发_Idea编译NIFI最新源码_详细过程记录_全解析_Maven编译NIFI避坑指南001---大数据之Nifi工作笔记0068
查看>>
NIFI汉化_替换logo_二次开发_Idea编译NIFI最新源码_详细过程记录_全解析_Maven编译NIFI避坑指南002---大数据之Nifi工作笔记0069
查看>>
NIFI集群_内存溢出_CPU占用100%修复_GC overhead limit exceeded_NIFI: out of memory error ---大数据之Nifi工作笔记0017
查看>>
NIFI集群_队列Queue中数据无法清空_清除队列数据报错_无法删除queue_解决_集群中机器交替重启删除---大数据之Nifi工作笔记0061
查看>>
NIH发布包含10600张CT图像数据库 为AI算法测试铺路
查看>>
Nim教程【十二】
查看>>
Nim游戏
查看>>
NIO ByteBuffer实现原理
查看>>
Nio ByteBuffer组件读写指针切换原理与常用方法
查看>>
NIO Selector实现原理
查看>>
nio 中channel和buffer的基本使用
查看>>
NIO_通道之间传输数据
查看>>